Tree 공부를 한 1주일째하는데 조각조각 배웠던것들의 퍼즐들이 조금씩 끼워 맞춰지는중. 아직 감이 다 안잡혔으나 오늘 헷갈렷던 개념중에 DFS(Depth First Search) vs BFS(Breath First Search) vs Traversal 개념이 혼동되어 큰 구조를 다시 잡아볼려한다.
내가 처음에 배웠던 1) In-order, 2) pre-order, 3) post-order 알고리즘의 개념은 DFS로 속하고 4) level-order traversal(Queue)를 사용하는것은 BFS 개념에 속한다. 이때 1,2,3) 알고리즘은 Recursion을 사용하지만 Stack을 사용해서도 나타낼 수 있다.
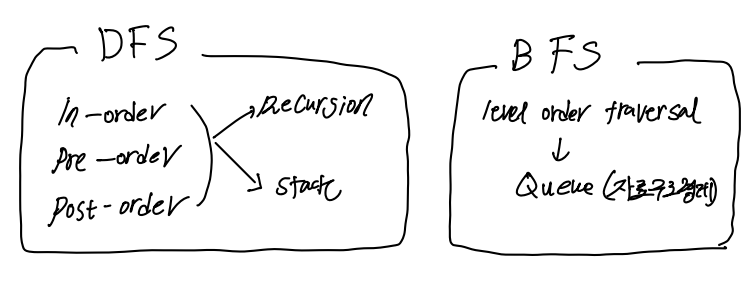
DFS 의 이미지!

여기서 다시한번 그림으로 Traversal들의 개념을 잡고가보자 (맨날 헷갈린다.)
자 아래표로 좀더 쉽게 구분지어보기 pre 접두사 는 before 란 의미를가지고 in은 안쪽 post 는 'after'로 생각!!!
| pre- | ROOT | left | right |
| in- | left | ROOT | right |
| post- | left | right | ROOT |
1)pre-order traversal
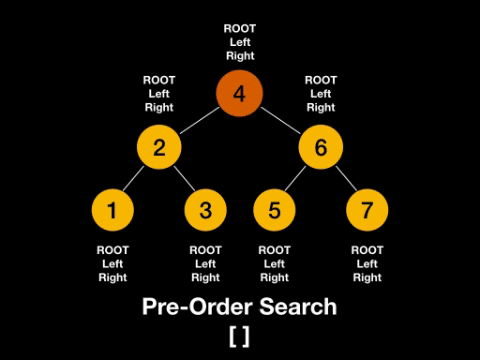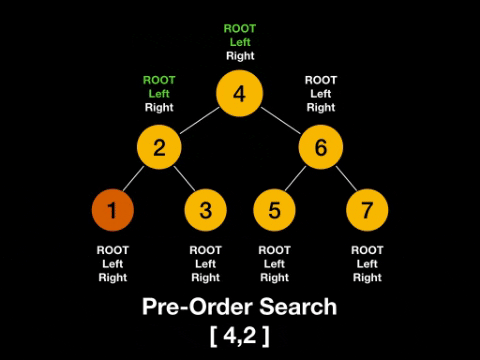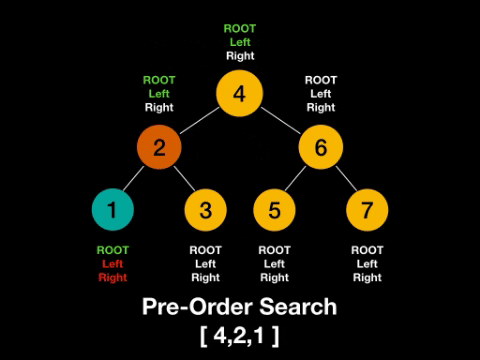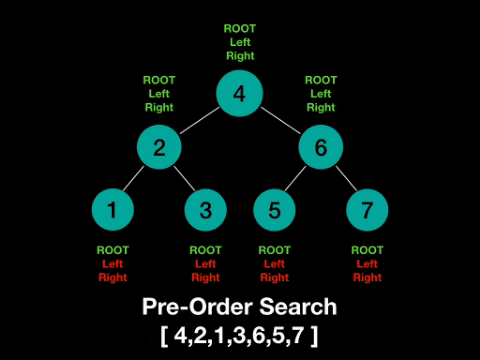
이를 코드로 표현하면 1) recursive version 이 있고 2) stack version이 있을수있다!
recursive version
void printPreorder(struct Node* node)
{
if (node == NULL)
return;
/* first print data of node */
cout << node->data << " ";
/* then recur on left subtree */
printPreorder(node->left);
/* now recur on right subtree */
printPreorder(node->right);
}stack version
void iterativePreorder(node* root)
{
// Base Case
if (root == NULL)
return;
// Create an empty stack and push root to it
stack<node*> nodeStack;
nodeStack.push(root);
/* Pop all items one by one. Do following for every popped item
a) print it
b) push its right child
c) push its left child
Note that right child is pushed first so that left is processed first */
while (nodeStack.empty() == false) {
// Pop the top item from stack and print it
struct node* node = nodeStack.top();
printf("%d ", node->data);
nodeStack.pop();
// Push right and left children of the popped node to stack
if (node->right)
nodeStack.push(node->right);
if (node->left)
nodeStack.push(node->left);
}
}2) In-order traversal

inorder도 또한 좌측노드부터 먼저 탐색되고 print(cout)의 위치로 달라지는 차이밖에없다.
3)Post-order traversal

BFS 이미지!

이는 구현방법이 Queue 로 표현하는것이 대표적이다. 같은 층을부터 아래로 순서대로 찾기때문에 4)level-order traversal이라고도 불린다. tree 에서 deletion을 구현할때 사용된다.
대표 c++ 코드
void printLevelOrder(Node* root)
{
// Base Case
if (root == NULL)
return;
// Create an empty queue for level order traversal
queue<Node*> q;
// Enqueue Root and initialize height
q.push(root);
while (q.empty() == false) {
// Print front of queue and remove it from queue
Node* node = q.front();
cout << node->data << " ";
q.pop();
/* Enqueue left child */
if (node->left != NULL)
q.push(node->left);
/*Enqueue right child */
if (node->right != NULL)
q.push(node->right);
}
}
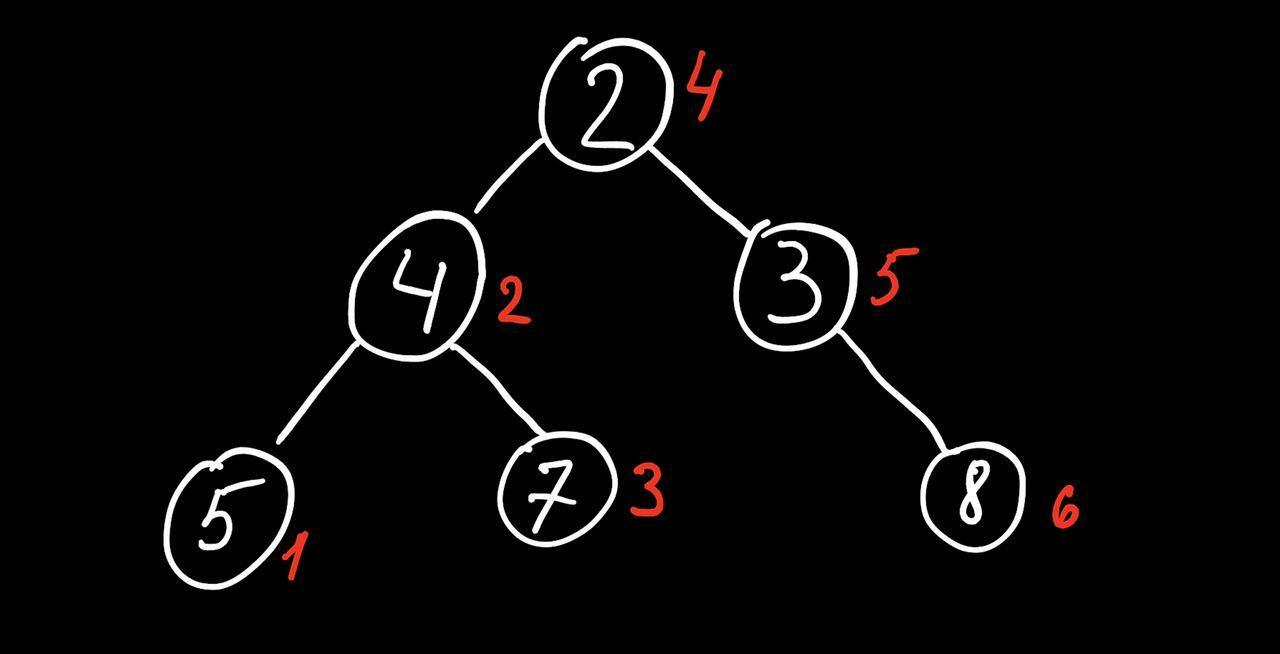
후.. 장황하지만 어느정도 퍼즐을 노력!!! stack 과 queue로 구현할떄는 직접 데이터 구조를 그려보고 하나하나 넣어보는 연습이 도움이된다. Traversal 순회하는 방법이 tree와 graph의 핵심인듯하다. 예를 들어 이렇게 말이다. 화이팅

'Data Structure & Algorithms > Trees and Graphs' 카테고리의 다른 글
| [Graphs] 개념 공부 (0) | 2023.02.07 |
|---|---|
| [Tree] Binary Search Tree (BST) not BTS (1) | 2023.02.06 |
| [Trees] Binary Tree Deletion 이해 (0) | 2023.01.25 |
| [Tree] 기초 inorder traverse 구현 및 이해 (0) | 2023.01.20 |
| [Graphs] BFS vs DFS 비교하기 (0) | 2023.01.18 |



댓글