오랜만에 다시 동기부여를 받고 코딩공부 !!!
오늘할것은 Binary Search Tree (BST) ! 값들을 저장할때 큰값과 작은 값을 좌우로 나누어 변경하여 굳이 전체를 찾을 필요가없는 데이터 구조 트리이다. 루트 노드 기준으로 찾고자하는값이 작으면 왼쪽 브랜치로 크면 오른쪽 브랜치로 이동하여 검색을 한다.
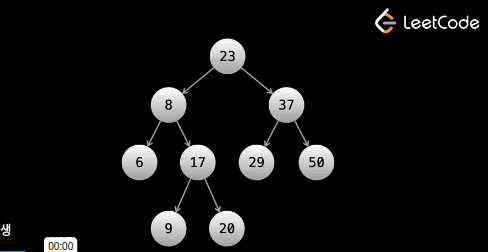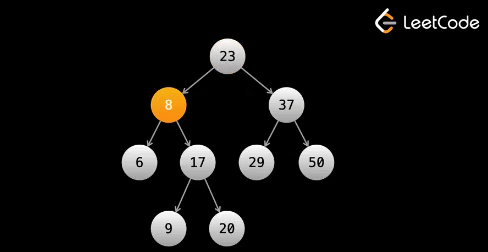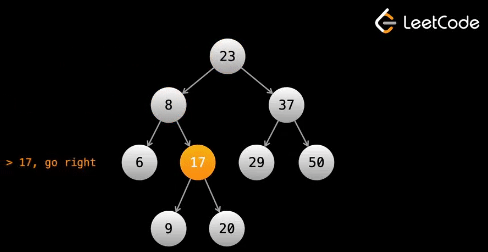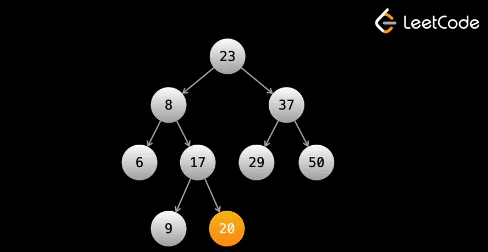
평균 시간은 time on average, Worst time : O(n) 이며 이때는 linked list처럼 찾고자하는 값이 트리의 끝단 레벨에 있는경우이다.
팁* 위 그래프에서 Inorder search(DFS) 를 한다면 정렬된 숫자가 출력된다. 예제로 차근차근 따라가 보자
대표문제1.) 938. Range Sum of BST
Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].
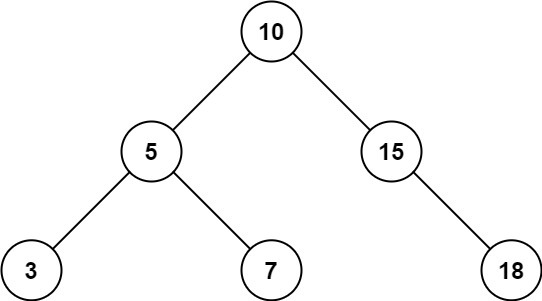
원하는것: 주어진 low, high값을 사이에 들어있는 모든 값의 합
TC : log(n) in average
1번 : Recursive 방법 (오! 이해가된다.)
class Solution {
public:
int rangeSumBST(TreeNode* root, int low, int high) {
if(root ==NULL){
return 0;
}
int sum = 0;
// BST로 접근한다 -> Recursion 방법;
if(root->val >= low && root->val <= high){
sum += root->val;
}
if(root->val >= low){
sum += rangeSumBST(root->left,low,high); // left recursive first;
}
if(root->val <= high){
sum += rangeSumBST(root->right,low,high);
}
return sum;
}
};
2. Stack 이용법
class Solution {
public:
int rangeSumBST(TreeNode* root, int low, int high) {
stack<TreeNode*> stack;
stack.push(root);
int ans = 0;
while (!stack.empty()) { // stack 이나 queue나 while문을 돌려주면서 끝내주는 조건입력필요
TreeNode* node = stack.top();
stack.pop();
if (low <= node->val && node->val <= high) {
ans += node->val;
}
if (node->left != nullptr && low <= node->val) {
stack.push(node->left);
}
if (node->right != nullptr && node->val < high) {
stack.push(node->right);
}
}
return ans;
}
};대표문제2.) 530. Minimum Absolute Difference in BST
Given the root of a Binary Search Tree (BST), return the minimum absolute difference between the values of any two different nodes in the tree.
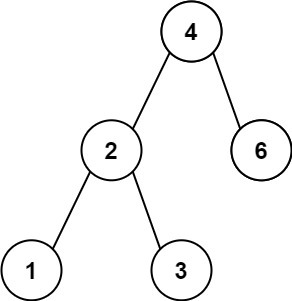
What: 붙어있는 두개 노드의 최소차이...
TC : O(n^2) - array 에 넣을경우 , O(n*logn) - sorted array를 사용할경우, O(n)- 팁에서 언급한 in-order traverse를 사용한다면
1번 방식 : Recursive
class Solution {
public:
int getMinimumDifference(TreeNode* root) {
vector<int> values = dfs(root);
int ans = INT_MAX;
for (int i = 1; i < values.size(); i++) {
ans = min(ans, values[i] - values[i - 1]);
}
return ans;
}
vector<int> dfs(TreeNode* node) { // dfs를 따로 쓸수있도록 백터화 해서 분리했네 ㄷ.ㄷ 예술
if (node == nullptr) {
return vector<int>{};
}
vector<int> left = dfs(node->left);
vector<int> right = dfs(node->right);
left.push_back(node->val);
left.insert(left.end(), right.begin(), right.end());
return left;
}
};
*STL tip*
vector_name.insert(position, iterator1, iterator2)- Parameter: The function accepts three parameters specified as below:
- position – It specifies the position at which insertion is to be done in the vector.
- iterator1 – It specifies the starting position from which the elements are to be inserted
- iterator2 – It specifies the ending position till which elements are to be inserted
2번 방법 : stack with in an in order traversal
class Solution {
public:
int getMinimumDifference(TreeNode* root) {
vector<int> values = iterativeInorder(root);
int ans = INT_MAX;
for (int i = 1; i < values.size(); i++) {
ans = min(ans, values[i] - values[i - 1]);
}
return ans;
}
vector<int> iterativeInorder(TreeNode* root) {
stack<TreeNode*> stack;
vector<int> values;
TreeNode* curr = root;
while (!stack.empty() || curr != nullptr) {
if (curr != nullptr) {
stack.push(curr);
curr = curr->left;
} else {
curr = stack.top();
stack.pop();
values.push_back(curr->val);
curr = curr->right;
}
}
return values;
}
};릿코드는 2번방법인 inorder DFS가 훨씩 복잡하기에 되도록 Recursive 방식을 차용하라고한다. 인터뷰에 두가지 방법을 물어볼 수 있지만 매우 드믈다고 한다. 이야... 머리에서 그림 그리기용
.
대표문제3.
: 98. Validate Binary Search Tree
Given the root of a binary tree, determine if it is a valid BST.
Example 2:
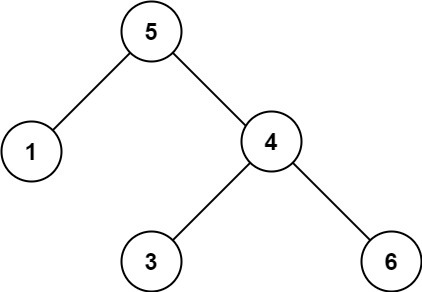
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.=> 내 사고 방식을 바꿔야하네 ... 완전 생각의 변환 와.. 내가 생각했던 방식은 root ->right ->val ,와 left가 root-val보다 작거나 큰것의 차이로써 해결하려고 했는데 이에 대한 문제가 무엇이냐 [5,4,6,null,null,3,7] 일 경우 잘못된값을 반환한다. 생각을 변환해서 BST의 특징인 왼쪽 섭트리값들은 부모 노드 보다 항상 값이 작아야하며 오른쪽 섭트리 값은 부모 노드보다 항상 값이 크다는것을 이용해야한다.
class Solution {
public:
bool isValidBST(TreeNode* root) {
return dfs(root, LONG_MIN, LONG_MAX);
}
bool dfs(TreeNode* node, long small, long large) {
if (node == nullptr) {
return true;
}
if (small >= node->val || node->val >= large) {
return false;
}
bool left = dfs(node->left, small, node->val);
bool right = dfs(node->right, node->val, large);
return left && right;
}
};과연 내가 이걸 다시 쓸수있을지 반복밖에 답이없다. 헑...
'Data Structure & Algorithms > Trees and Graphs' 카테고리의 다른 글
| [Graphs] Graphs- DFS - Number of Provinces (0) | 2023.02.08 |
|---|---|
| [Graphs] 개념 공부 (0) | 2023.02.07 |
| [Trees] Traversal 개념과 DFS, BFS 개념 혼동 정리 (0) | 2023.01.27 |
| [Trees] Binary Tree Deletion 이해 (0) | 2023.01.25 |
| [Tree] 기초 inorder traverse 구현 및 이해 (0) | 2023.01.20 |


댓글