Objectives
- Define the structure of a deep feedforward network
- Be able to choose and justify different activation functions for hidden layers and the output layer.
- Explain the backpropagation algorithm
Tutorial

- deep forward network를 수학적 표현
- ReLu 를 수학적으로 표현.
Part1:Deep feedforward network definition

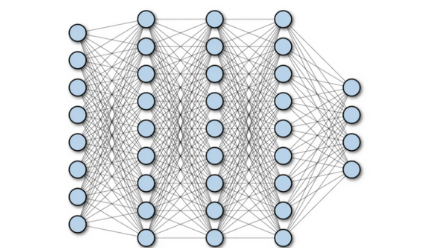
- Feedforward network : 피드백을 받지않고 이전 레이어에서 다음 레이어로 앞으로 전달만해주는 뉴럴네트워크 개념.
- 첫번째 레이어의 뉴론은 두번째 레이어의 뉴론들에 다 연결되어 있는 특징. 여기서 Fully connected layer라는 개념출현.
- 여기서 hidden layer라는 용어는 말그대로 여러 레이어들이 숨겨져있다는말. 위 도표 many layers들이라 할 수있음.
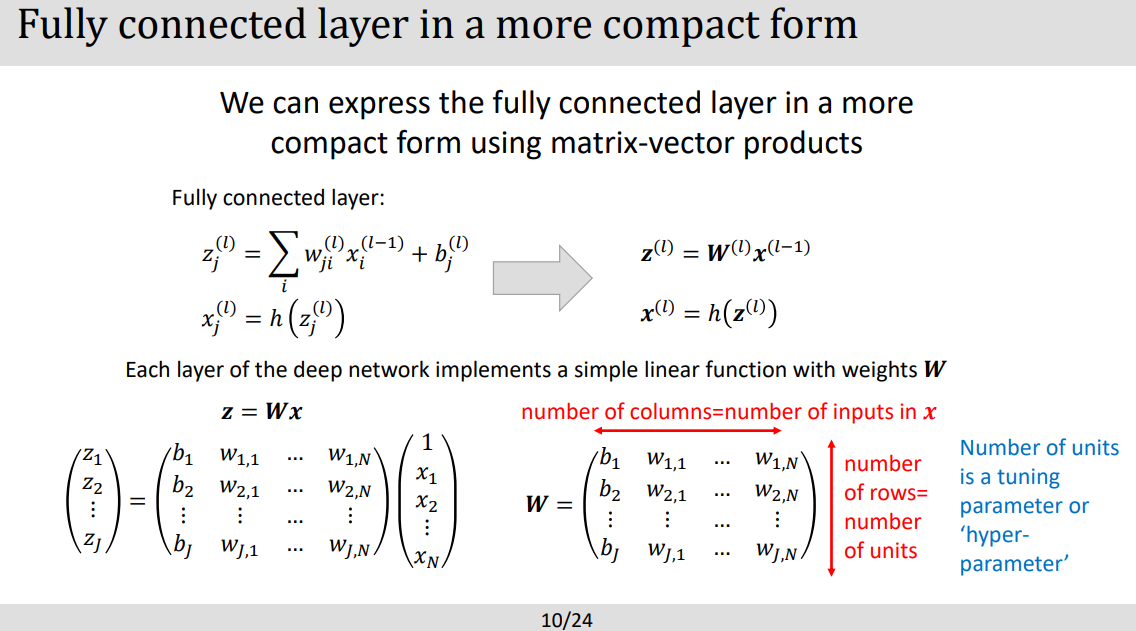
- j 는 units들의 갯수로 hyperparameter라고 칭함
- 튜토리얼 출제, 시험문제에서도 더 심화되어 출제된 개념으로 숙지
- 몇개의 fully connected layer 가 쓰이는지 어떻게 정해?
- 일반적으로 정확히 정해진게 없이 단순하게 직접 넣어보면서 정해봐야한다. 너무 많은 요소들이 영향을 끼치기 떄문에. 밑에는 어떤 요소들을 봐야하는지 설명
- 문제의 복잡도를 고려 : 문제가 단순하다면 한두개의 레이어로도 가능하지만 문제가 복잡하다면 여러개의 레이어가필요. 여기서 문제란? 이것도 여러 요소가 있는데 도메인을 이해하고 인풋 데이터의 사이즈나 퀄리티를 이해도 필요. 또한 카테고리의 클래스 갯구도 고려하고 딥러닝 아키텍쳐도 고려해야한다함… =? 아니 그럼 어떻게 최적화된 레이어를 구해? 일단가장 단순한방법으로는 적은 레이어로부터 갯수들 늘려가서 퍼포먼스 경향을 보라고하네 .
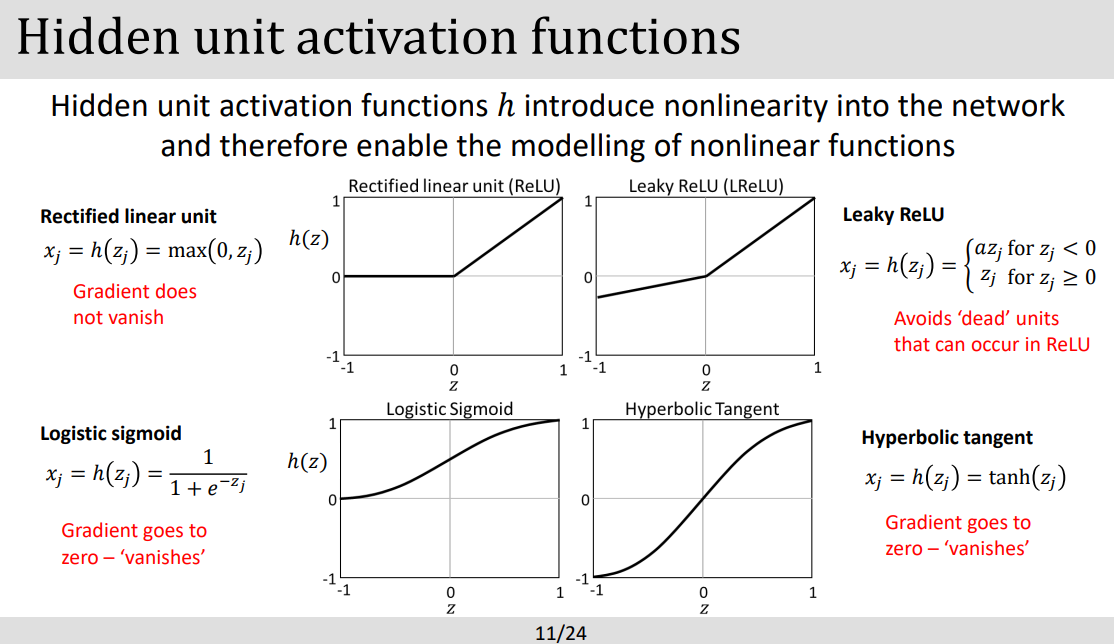
- **Activation function 개념:
- 목적: 왜 Activation function 은 non linearity의 성질을 도입하였지? ⇒ 세상은 non linear하기에.. non linear한 모델을 찾기 위해서!. (인풋과 아웃풋 데이터의 더 복잡한 관계를 표현하기위해)
- 좀더 깊게 작동 원리에 대해 보자면 activation function(활동 함수)는 Input 데이터들의 가중치된 합(weighted sum)을 활용하는데 이때 bias(편향)을 추가하여 non-linear한 값을 뉴런의 Output 으로 반환하는 원리이다.
- z 는 아웃풋 , x 는 인풋, w 는 가중치, b 는 bias 라고 이해, h 는 hidden activation function의 약자.

- 저 chain rule 숙지하기

- 위 그래프에서 ReLU는 layer가 아니라 fully connected layer에 non-linearity 특성을 부여해 복잡한 모델을 더 다양하게 접근할수있도록 도와줌. ⇒ 활성 함수가 없다면 모델이 선형적 인풋 조합으로 밖에 만들지못해 다양한 해석을 할 수 없게 된다!
part2: Parameter estimation and backpropagation

- Backpropagation 의 목적 : Loss function의 값을 최대한 낮취기위해 기울기(gradient decent)(미분하는방식) 를 이용해 네트워크들의 weight와 bias을 조절찾는 방법으로 Loss로 부터 역으로 추적한다.
- 기울기가 계산될때 최적화 알고리즘으로 유명한 SGD (Stochastic gradient decent)를 사용해서 weight 과 bias를 반복적으로 돌며 업데이트 해준다.
- 위도표 설명으로 feedforward network로 중간중간 fully connected layer와 activation function(ex. ReLu)와 같이 이용해 마지막 loss를 계산하고 이때 loss function으로 부터 역으로 chain rule 미분을 이용해 각 뉴런들사이의 weight과 bias를 재조절하여 모델에 업데이트한다.
⇒ Backpropagation 과 activation function과 헷갈렸던부분은 활성함수는 non-linearity 특성을 부여하고 weight과 bias에 영향을 주지않는다 Backpropagation은 weight과 bias를 최적화하여 조절해준다 ⇒ 그럼 초기 weight과 bias는 어떻게 결정? ⇒ 랜덤하게 결정된다고한다.
- [추가 궁금증]그렇다면 미분을 하면서 발생하는 문제 ‘Vanishing gradient problem’란 무엇인가!!
- backpropagation 시 기울기가 점차 작아져 학습이 어려워지는현상을 말한다. (미분이 계속되는것 기억) . 이러한 작은 기울기는 모델이 학습 데이터에서 미세한 패턴을 찾아내는데 어려움을 줄수 있는데 이를 방지하기위해 ReLu를 사용하는데 입력값이 0보다 작을때는 기울기가 0이되지만 이보다 큰경우 기울기가 일정하게 유지되어 vanishing gradient현상을 막을수있다.




- 위 수학적 식이좀 빡세긴한데.. past paper를 살펴보며 어떤식으로 나오는지 비교하고 공부하기!.
'[End]Robotics Lectures in UoS > Deep Learning' 카테고리의 다른 글
| [DL] Lecture6:Deep learning for computer vision (0) | 2023.05.06 |
|---|---|
| [DL] Lecture5: Convolutional Networks (0) | 2023.05.05 |
| [DL] lecture4: Optimization and Regularization Techniques (0) | 2023.05.05 |
| [Deep Learning] lecture2 Machine Learning Fundamentals-시험준비 (0) | 2023.05.04 |
| [Deep Learning] 코스 시작! (0) | 2023.02.10 |




댓글